
Thus, the lateral surface area of an isosceles triangular prism is LSA = 2la + lb. Therefore, the total area of the three rectangles = 2la + lb Thus, the area of the third rectangle = l × b Let the length of the third rectangle is "l" units and the breadth of the third rectangle = 'b' units Thus, the area of the two congruent rectangles = 2 × l × a Let the length of the congruent rectangles is "l" units and the breadth of the congruent rectangles is "a" units. So let's first find the area of the 2 congruent rectangles: Since we already know that in an isosceles triangular prism, there are 2 congruent rectangles.

⇒ Area of two isosceles triangles = 2 × 1/2 × b × h = b × h

Let us consider an isosceles triangle with the equal sides be "a" units, the base of each of the triangle be "b" units and the height of the triangle is "h"Īrea of an isosceles triangle = (1/2 × base × height) = 1/2 × b × h The surface area of the isosceles triangular prism is found as SA = Sum of areas of 2 isosceles triangles at the bases + Sum of the areas of the 3 rectangles. The lateral area of an isosceles triangular prism is found as Lateral area, LA = Sum of the areas of all the vertical faces = Sum of the areas of the three rectanglesĭerivation of Surface Area of Isosceles Triangular Prism

Since we know that the vertical faces in the case of an isosceles triangular prism are rectangles, therefore, to find the lateral area we will have to find the areas of all the vertical faces and then add them up. Lateral Area refers to the total area of the lateral or vertical faces of any solid. ⇒ SA = Sum of areas of 2 isosceles triangles + Sum of the areas of the 3 rectangles The surface area of an isosceles triangular prism is found as SA = Sum of areas of all the faces To find the surface area of an isosceles triangular prism, we will have to add the areas of the 2 isosceles triangles at the base facing each other and the area of the rectangles formed by the corresponding sides of the two congruent triangles. The surface area of an isosceles triangular prism refers to the sum total of the area of all the faces of an isosceles triangular prism. Let us solve some examples to understand the concept better.Formula for Surface Area of Isosceles Triangular Prism Total Surface Area ( TSA) = ( b × h) + ( s 1 + s 2 + s 3) × l, here, s 1, s 2, and s 3are the base edges, h = height, l = length The formula to calculate the TSA of a triangular prism is given below: The total surface area (TSA) of a triangular prism is the sum of the lateral surface area and twice the base area. Lateral Surface Area ( LSA ) = ( s 1 + s 2 + s 3) × l, here, s 1, s 2, and s 3 are the base edges, l = length Total Surface Area
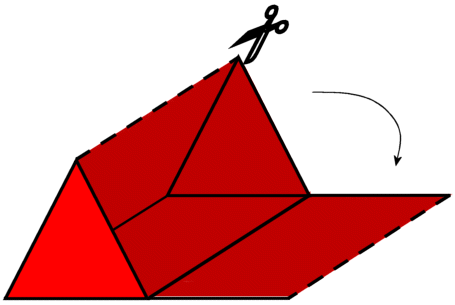
The formula to calculate the total and lateral surface area of a triangular prism is given below: The lateral surface area (LSA) of a triangular prism is the sum of the surface area of all its faces except the bases. It is expressed in square units such as m 2, cm 2, mm 2, and in 2. The surface area of a triangular prism is the entire space occupied by its outermost layer (or faces). Like all other polyhedrons, we can calculate the surface area and volume of a triangular prism. So, every lateral face is parallelogram-shaped.


 0 kommentar(er)
0 kommentar(er)
